f #note
Cour 5 dérivée
Taux de variation moyen
Le tauxx de variation moyen d’une fonction sur une intervale est donné par l’expression :
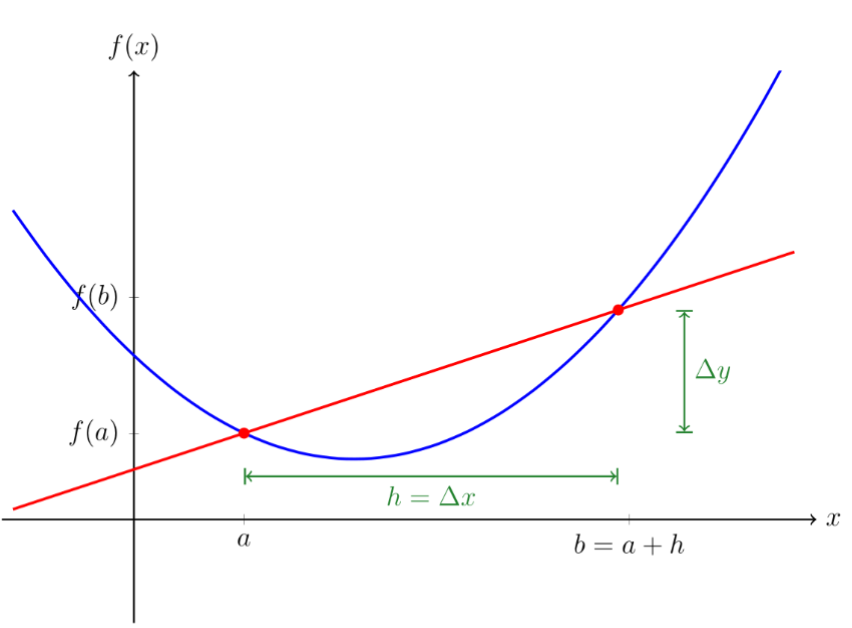
Fig. 1 : Example de taux de variation moyen
Ont peut également reformuler cette équation a partir de la valeur de et de la longeur de notre interval, (Ou ). Notre formule reformuler est donc :
Graphiquement
Ont peut voire cela comme la pente de la fonction affine qui passe par les points et . Ont nomme cette fonction affine comme la sécente qui passe par les deux extremiter de l’interval
Connection avec la physique
Cette séquence correspond également a la vitesse moyenne dans l’interval.
Taux de variation instantané
Taux de variation instantané est un oxymore
Tel ont n’atein jamais la valeur d’une limite, ont ne trouve jamais le taux de variation instantaner, simplement ce qu’elle approche avec le temp.
Pour imagine le taux de variation instantaner, ont eut prendre le taux de variation moyen pour un interval d’une longeur et rapetiser . Le taux de variation instantaner ce que le taux de variation moyen approche dans la limite quand tend vers zero. Ont nomme la fonction affine dans ce cas si la tangente.
Il peut être défenit comme ce suis :
Ou bien en utilisant plutot que
Dériver en un point
La dérive d’une fonction en un pint est le taux de variation instantatione de la fonction en .
C’est donc la pente de tengente en ce point.
Ont la note (dite prime) ou
Ont peut la donner par l’expression :
De la même faco nque pour les taux de variation, ont peut également écrire :
La (fonction) dérivée
La dérivée d’une fonction est en soit une fonction qui donne le taux de variation instantaner pour le point .
Ont peut la donné d’une des maniere suivante , , ou .
est donné par :
Ont peut remlacer par
Il y a certaine fonction qui ont des point noin-dérivable. Par example, le point au font du “V” dans une fonction valeur absolue n’est pas dérivable, car il y a un changement instantaner dans le deriver, et ont ne peut pas defenir de tangante. Ont dit donc que le deriver est non continue. Ont peut cependant defenir un deriver pour tout les point de la fonction autre que le point il y a discontininuiter.
Théoreme
Si une fonction est dérivable en alors elle est continue en
Une fonction est donc non-dérivable en un point si l’une des trois contition est satisfaite :
- La fonction est non-continue en (asymptote, saut, ect)
- La fonction est continue en , mais change brusquement de dirrection en ce point (le derivé est non-continue)
- Si la tangente est verticale en (cusp)