f #note
dérivation implicite
Certaines fonction sont dite “implicite”, soit des fonctions qui ont et d’un côter de l’égaliter. Par example :
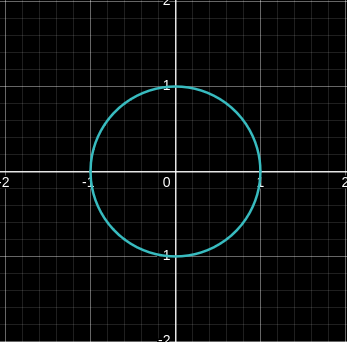
Defenit une courbe implicite qui est un cercle.
Fig. 1
Ont nomme dérivation implicite le processus de trouver la pente de tangente d’une tengente sur le cercle.
Dérivation implicite d’une fonction
Pour dériver une fonction implicite, il faut :
- Dériver la fonction par rapport a l’une des deux variables, en considerant que l’une est une fontion de l’autre
- Isoler les termes du styles
Par example
Consideront la fonction , donc nous souhaitont trouver Pour rendre cella extra clair que serat considerer comme une fonction de , je vais dénoter comme étant . est une fonction dérivable, mais dont nous ne conaisont pas la forme. Notre fonction est donc . Ont cherche donc a trouver
- Premierement, nous dérivont par rapport a , comme ceci.
- A noter que ici nous avont dériver selon la regle de la chaine, car nous aviont composer dans la fonction
- Ont peut ansi remplacer par
- Remarquont que l’ont a put dériver , sans jamais savoir ce qu’était
- Ensuite, ont peut isoler