la dérivée 2025-09-09

f #note

$Created:2025-09-09$

La (fonction) dérivée

La fonction dérivé est une généralisation du dériver en un point. Intuitivement, le dériver est défenit comme étant une fonction $f^{\prime }(x)$ (prononcer “f” prime de x), qui, pour toute valeur de $x$ est égale a la valeur du dériver en un point pour ce point $x$, si il existe.

Ont peut le noté avec une notation permis celles ci : $f^{\prime }(x)$, $y^{\prime }$, $\frac{df}{dx}$ ou $\frac{dy}{dx}$.

Plus formelement, ont peut de defenir comme il se suit :

$$f^{\prime }(x)=\underset{\Delta x\to 0}{\lim }\frac{f(x+h)+f(x)}{\Delta x}$$

A noter que le $\Delta x$ peut être également dénoter $h$

Fonctions et points non-dérivable

Une fonction peut être non-dérivable en parti ou dans son entiereter (Ont étudie pas encore les fonction entirement non-dérivable). Si un point d’une fonction répond a l’un des trois critères suivants, alors elles est non-dérivable en ce point :

• La $f$ n’est pas continue en $x=a$
  • Par example, si il y a asymptote, saut, ect
• Si la fonction $f$ est continue en $x=a$, mais qu’elle quange brusquement, alors elle n’a pas de deriver
  • C’est le cas par example de la fonction valeur absolue
  • Plus formelement, ont dit que le deriver de la fonction n’est pas continue. Encore plus formelement, la limite de $x\to a$ n’est pas defenit pour la dérivée
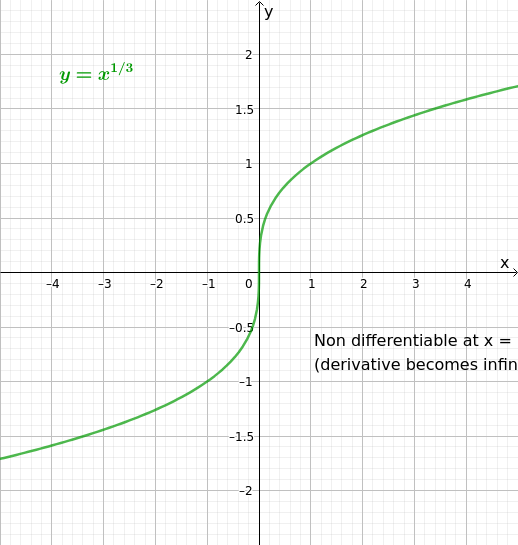
• Si la tangente est virticale en $x=a$
  • C’est une espece de crête

Figures : Examples de fonctions non-diferentiables

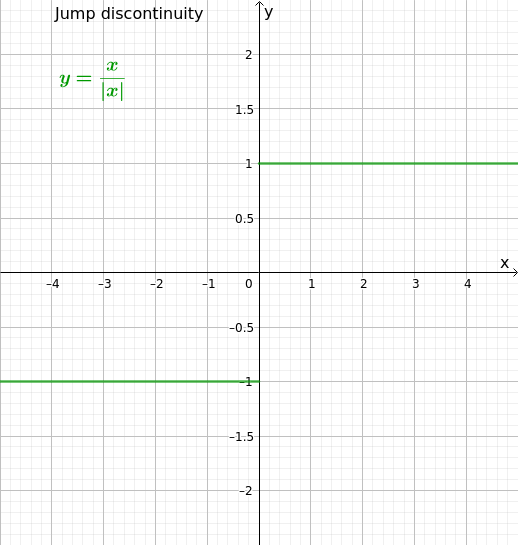
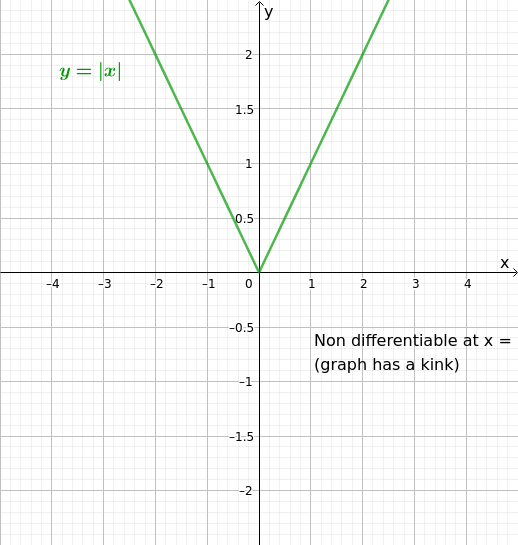
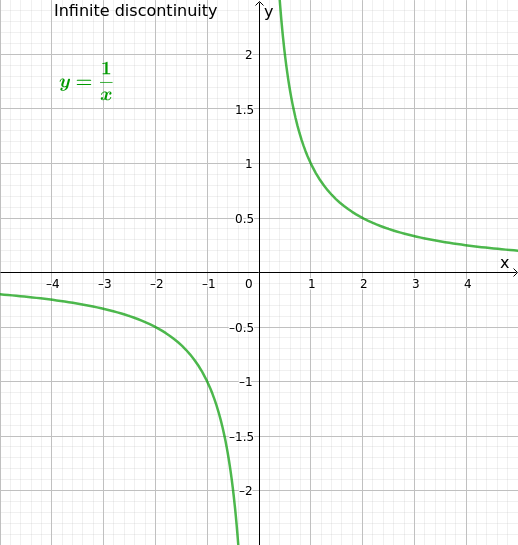
Infomration suplémentaires

Il y a deux types suplémentaires de fonction non diferentiables que l’ont ne vois pas, soit les fonction “bizarres” (oui c’est le terme), par example une fonction qui est 1 pour les nombre rationels et 0 pour les nombres irationels C’est également le cas des fonctions qui ne sont pas “nice”, par example $\sin \left(\frac{1}{x}\right)$ (la fonction ne peut pas wigle trop rapidement)