f #note
Extremums relatifs
Ont peut clairement observer des extremums graphiquement sur certaines fonction.
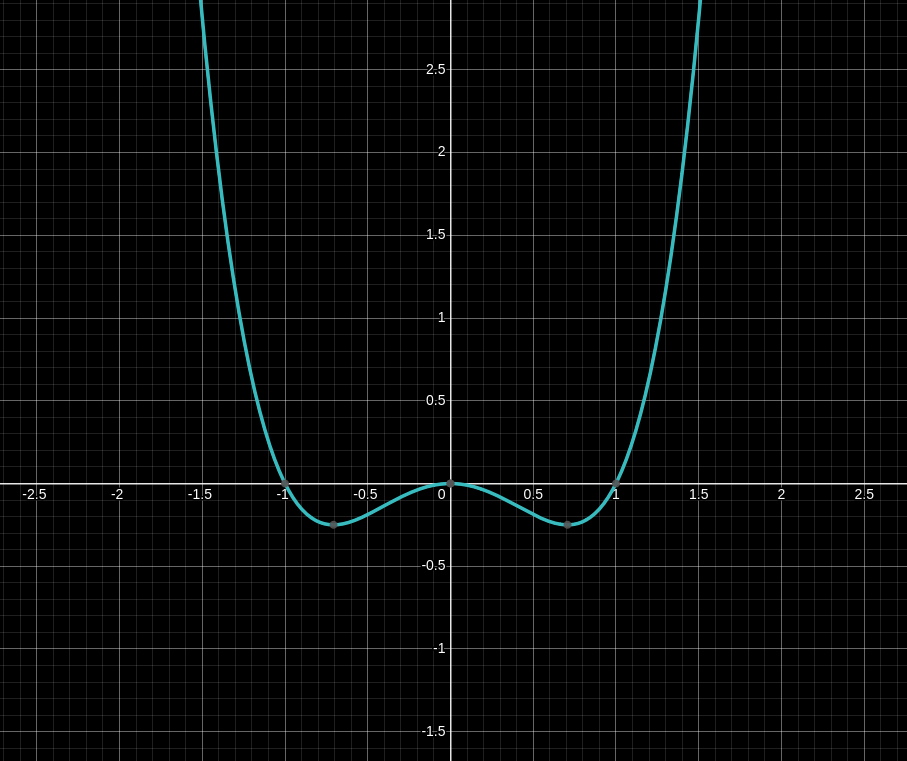
Fig. 1 : Un graphique avec des extremums relatifs
Ce ne sont pas des maximums et minimum dans le sens traditionell (en tout cas pas tout le temp), mais ils sont localement des max ou min.
Ont peut formaliser cette intuition visuelle en remarquant que d’un côter d’un extremum relatif, la courbe augmente ou diminue, et de l’autre, c’est l’inverse. Les extremums relatifs sont donc les endroits la dériver de la courbe change de signe
Ont peut observer ceci dans le diagrame suivant :
Fig. 1 : Démonstration d'extremums relatifs
Ont peut voire en orange notre graphique initial, en rose la dériver de ctte fonction, et les traits blui sont les points ou la dériver égale zero. Dans ce graphique ci, la dériver change de signe, mais ce n’est pas néséairement le cas
Ont nomme cette métode pour trouver des extremums relatifs le test de la dériver premiere
Point critique
Unt nomme valeur critique une valeur du domaine d’une fonction tel que sont dériver est égale a zero (ou n’existe pas). Formelement :
Defenition de valeur critique
Une valeur telle que ou est nommer une valeur critique que Si est une valeur ctritique de , alors nous dirons lque le point est un point ctritique
Formalisation
Ont peut formaliser cette notion comme ce suit :
Defenition d'un extremum relatif
Soit une fonction et Ont dit que possède un maximum relatif en si il existe un intervalle ouvert contenant tel que Ont peut généraliser ceci pour min également en inversant le
Ont peut également formaliser le test de la dériver premiere :
Defenition du test de la dériver premiere
Soit une fonction continue sur un intervalle et dérivable sur (sauf parfois en ) ou , telle que soit un point critique de Si dans l’intervalle et dans l’interval alors possède un mimimum relatif en .