Limite 2025-09-06

f #note

$Created:2025-09-06$

Limite

Une limite est quand ont as une fonction qui approche une certaine valeur de plus en plus. Par example, la fonction $\frac{1}{x}$ devient de plus en plus proche de $0$ plus $x$ augmente. Ont dit donc que la limite de $\frac{1}{x}$ approche $0$ quand $x$ s’approche de $\infty$.

Fig.1 : Graphique de $\frac{1}{x}$

(Les lignes pointiller sont les asymptote)

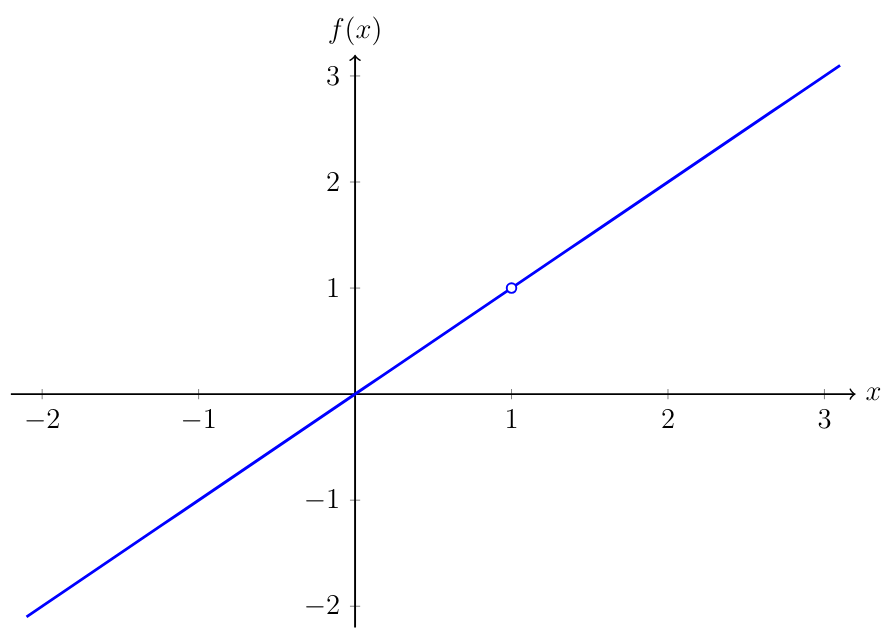
Ont peut également approcher un point fixe, par example, dans le graphique suivant, ont peut approche le point $x=1$.

Fig. 2 : Deuxieme example

Ont peut également voir qu’il n’est pas nésésaire que la fonction soit defenit dans notre point.

Ont peut approcher notre point dans deux direction, soit en approche a partir de la gauche, ou de la droite. Une limite est uniquement defenie si la limite est la même en approchant de la gauche et de la droite. Dans le deuxieme example, la limite ets égale a 1

Notation algébrique

Ont dénote une limite comme ceci :

$$\underset{x\to a}{\lim }f(x)=L$$

Ou :

• $x$ est la variable qui change
• $a$ est la valeur que $x$ approche
• $L$ est le resultat de la limite
• $f(x)$ est la fonction sur laquel ont approche la limite.

Ont peut également dénoter la direction dont ont approche le point $a$ de la maniere suivant :

• $x\to a^{-}$ : Ont approche $a$ de la gauche
• $x\to a^{+}$ : Ont approche $a$ de la droite

Existance d’une limite

Une limite existe seulement si les conditions suivante sont satisfaite :

Soit $f$ une fonction et $a$ un nombre réel, $I$, un interval ouvert tel que $a\in I$ et $I\setminus \{a\}\subseteq dom(f)$.

Ont dit que \lim_\limits{x \to a}f(x) \exists si et seulement si \lim_\limits{x \to a^+}f(x)=\lim_\limits{x \to a^-}f(x)=L ou $L\in \mathbb{R}$